|
Tan Liang Soon and Hang Kim Hoo

Introduction
At the heart of learning math, it is always about learning correctly, accurately, and comprehensively, so that students will acquire the competencies to engage in lifelong and self-directed learning in math. This in turn can support their future work in the transformed economic landscape of Singapore brought about by the fourth industrial revolution. In Singapore, mathematics is a compulsory subject for students from primary one (Year 1) to end of secondary schooling (typically Year 10). In addition to mathematical concepts and skills, the Singapore mathematics curriculum also involves the learning of mathematical processes, of which mathematical problem solving occupies a central position. In this article, we focus on three aspects of the pedagogical practice of mathematical problem solving in Jurong Junior College (JJC), namely, learning for math problem solving, learning about math problem solving, and learning through math problem solving.
Learning for Math Problem Solving
Overcoming the challenges in teaching and learning for conceptual understanding can be a complex pedagogical problem, particularly in the introduction of more advanced mathematical concepts. Yet, overcoming such pedagogical challenges is essential for students to be equipped with the mathematical concepts required to solve math problems. According to Tall and Vinner (1981), math concepts can be viewed as network of nodes with connections to students’ concept images. A student’s concept image is described as “the total cognitive structure that is associated with the concept” (Tall & Vinner, 1981, p. 152), and can span a student’s mental images of the concept, its associated properties, his experiences with the concept, and the processes involved. In the course of forming the concept images, cognitive conflicts that interfere with their use of the concept definitions in mathematical arguments can arise. The ways in which these cognitive conflicts are resolved through students’ learning experiences can determine the coherence and depth of understanding of the concept. We present a case example to illustrate students’ formation of concept images for Linear Spaces in a Further Mathematics classroom.
In the teaching and learning of Linear Algebra in the Further Mathematics classroom, we anticipated the difficulties our students may face when trying to understand the inherent abstract concepts. The lessons were designed to augment students’ understanding of the formal definitions of Linear Transformation, Null Space, and Range space with computer visualizations of the key ideas involved. We were of the view that didactic teaching of the concept definitions alone was necessary but not sufficient for students to develop the requisite conceptual understandings for solving the problems in Linear Algebra. Computer visualizations were thus used to enrich students’ learning experiences so that they can develop more appropriate and coherent concept images. Such pedagogical practices positively influenced students’ formation of concept images. As shown in Fig 1, students demonstrated part of their concept images through the production of videos on Linear Transformation and Null Space. Readers can scan the QR code provided to view the video.
Learning about Math Problem Solving
The practice of math problem solving is central to the discipline of mathematics and the nature of mathematical thinking. It constitutes the core of math education in Singapore and around the world. The development of math problem solving competencies in our students are therefore of paramount importance. For this purpose, a framework comprising a set of guiding questions (see Table 1) was developed based on the problem solving heuristics suggested by Polya (1957). Students were provided with this set of questions to guide their problem solving during lecture and tutorial discussions. It also served as a guide for teachers to model the math problem solving process for students.
As shown in Table 1, the first question of the framework requires students to understand what is required of the problem situation. A sketch of the problem situation can help to enhance students’ understanding of the problem. During class discussion of tutorial problems, some teachers found it useful for students to first read out the math problem aloud and then underline the key information provided before sketching out the problem situation. Answering this question would sometimes entail the reformulation of a complex problem into a related but simpler problem. An example would be students reformulating 3D Vector problems into the more accessible 2D Geometry problem situations.
The second question is intended for students to be sensitized to the mathematical practice of noticing important math variables, structures and relationships that can be used to formulate the problem solution. The formulation of the problem solution would also require students to connect key ideas across various math topics.
The third question aims to inculcate in students the learning habits of evaluating the reasonableness of one’s problem solution and the open-mindedness to explore more elegant alternative solutions. The fourth question is to encourage students to pose new problems by examining and varying the problem conditions and constraints. The underlying questions used in this problem posing process are “What if” and “What if it’s not the case that”. The third and fourth questions in this framework are related to the “Looking back” phase of math problem solving as discussed by Polya (1957).
It is noted that this set of guiding questions for math problem solving is iterative in nature, in that the “Looking back” process as suggested by the third and fourth questions are intended to help improve students’ abilities to handle the first two questions when faced with complex novel problem situations. The “Looking back” process would engage students in variation practice which in turn could develop greater mathematical insights and refine one’s concept images necessary for solving more complex problems. Studies on the impact of the framework on the efficacy of students’ math problem solving are ongoing.
Learning through Math Problem Solving

The math interest group in our college was formed in response to the need to cater to students’ diverse passion and interests in math related activities, of which math research projects is a part. We describe students’ engagement in one math research project (see Fig 2) to elucidate our pedagogical practice for students to learn through math problem solving.
The math research group students were varying the skips conditions for the “Candies Problem” that was posed as the 2015 Singapore Mathematics Olympiad Senior Round 2 question:

In particular, the students investigated the solutions to the three specific cases of skip sequences: the arithmetic progression, the geometric progression and the Fibonacci sequence. They formulated the problem solutions for these variations in the form of the general congruence equation: 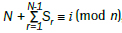 , where the solution of the congruence solution i denotes the location of the N th sweet for the particular type of skips sequence denoted by Sr. , where the solution of the congruence solution i denotes the location of the N th sweet for the particular type of skips sequence denoted by Sr.
In the case of the arithmetic progression, the students obtained the following results:

Through the process of proving these results, the students learnt among other things, Fermat’s last theorem and Modular exponentiation using Euler’s theorem.
As another case example, some students in the H2 Mathematics classroom were varying pairs of line equations for obtaining the vector equation of the plane. Through this “Looking back” process, they learnt that a pair of skew lines serve as a counter example to their original claim that any pair of line equations can be used to obtain the equation of the plane that contains them.
Conclusion
Our discussion on the pedagogical practices of math problem solving in Jurong Junior College suggest that math problem solving as a learning experience need not be reserved for students with exceptional math abilities. In fact we posit that math problem solving should be the salient feature of the complete math learning experiences for all students. That is, in the world of math, there is always a place for everyone.
Dr Tan Liang Soon is Head of Mathematics at Jurong Junior College. Dr Hang Kim Hoo is Principal of Jurong Junior College .
For more information about this article, please contact Dr Tan Liang Soon at tan_liang_soon@moe.edu.sg
References
Polya, G (1957) How to solve it (2nd ed ). New York: Doubleday
Tall D.O. & Vinner S. (1981) Concept image and concept definition in mathematics, with special reference to limits and continuity, Educational Studies in Mathematics, 12 151-169.
 Click here to download the full issue for USD 6.50 Click here to download the full issue for USD 6.50
|





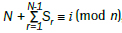 , where the solution of the congruence solution i denotes the location of the N th sweet for the particular type of skips sequence denoted by Sr.
, where the solution of the congruence solution i denotes the location of the N th sweet for the particular type of skips sequence denoted by Sr.

 Click here to download the full issue for USD 6.50
Click here to download the full issue for USD 6.50